Aproximación Informal a los Limites
El límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Este término también se utiliza para nombrar a una restricción o limitación, al extremo que se puede alcanzar desde el aspecto físico y al extremo a que llega un periodo temporal.
Una definición informal del límite matemático indica que el limite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea tan cercano a T como se pretenda. Además del límite citado, no podemos obviar que existen otros muy importantes en el ámbito de las Matemáticas. Así, también se puede hablar del límite de una sucesión que puede ser existente o único y divergente, en el caso de que los términos de aquella no converjan en ningún punto.
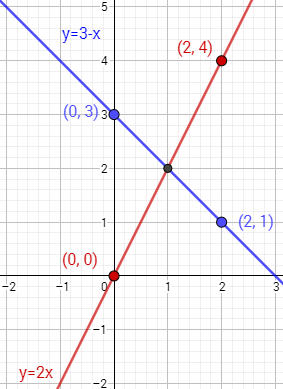
En las siguientes gráficas, se puede observar que para calcular limx→cf(x), es decir, el limite de una función f(x), cuando x tiende al valor c, no es necesario que la función esté o no definida en c, lo que interesa es que festé definida en las cercanías de c.
Ejemplo 1. La función f está definida para "todos" los valores alrededor de un número "c", incluso en el punto c mismo.

Aunque no es necesario que la función esté definida incluso en c mismo, se observa que cuando x→c, entonces, f(x)→L, es decir, cuando "x tiende a c", entonces "f(x) se aproxima al número L".
En este caso, se dice que el límite exite y se escribe como: limx→cf(x)=L
El límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros.
Este término también se utiliza para nombrar a una restricción o limitación, al extremo que se puede alcanzar desde el aspecto físico y al extremo a que llega un periodo temporal.
Una definición informal del límite matemático indica que el limite de una función f(x) es T cuando x tiende a s, siempre que se puede hallar para cada ocasión un x cerca de s de manera tal que el valor de f(x) sea tan cercano a T como se pretenda. Además del límite citado, no podemos obviar que existen otros muy importantes en el ámbito de las Matemáticas. Así, también se puede hablar del límite de una sucesión que puede ser existente o único y divergente, en el caso de que los términos de aquella no converjan en ningún punto.
En las siguientes gráficas, se puede observar que para calcular limx→cf(x), es decir, el limite de una función f(x), cuando x tiende al valor c, no es necesario que la función esté o no definida en c, lo que interesa es que festé definida en las cercanías de c.
Ejemplo 1. La función f está definida para "todos" los valores alrededor de un número "c", incluso en el punto c mismo.

Aunque no es necesario que la función esté definida incluso en c mismo, se observa que cuando x→c, entonces, f(x)→L, es decir, cuando "x tiende a c", entonces "f(x) se aproxima al número L".
En este caso, se dice que el límite exite y se escribe como: limx→cf(x)=L
Ejemplo 2. En este ejemplo, la función f no está definida para x=c.

Aunque f(c)≠L, se tiene que f(x)→L, para los valores de x cercanos a c.
Al igual que el caso anterior, el límite existe y se puede escribir: limx→cf(x)=L
Esto es, cuando x→c+, entonces f(x)→S, pero cuando x→c−, entonces f(x)→R.

En este caso, la función no tiende a un mismo valor cuando x se acerca a c, en consecuencia limx→cf(x), no existe.
Ejemplo 4. En este ejemplo, cuando "x tiende a c" por la derecha la función toma valores positivos cada vez mayores, mientras que cuando "x tiende a c" por la izquierda, la función toma valores positivos cada vez menores.
Esto es, cuando x→c+, entonces f(x)→+∞, pero cuando x→c−, entonces f(x)→−∞.

De lo anterior se deduce que la función no tiende a ningun número real fijo, cuando se acerca a c, en consecuencia limx→cf(x), no existe.

 , donde
p
(
x
) y
q
(
x
) son polinomios y
q
(
x
) ≠ 0.
, donde
p
(
x
) y
q
(
x
) son polinomios y
q
(
x
) ≠ 0.

 y la gráfica es una
hipérbola
.
y la gráfica es una
hipérbola
. 

 es –3. Esto es, cuando
x
= –3, el valor de
y
no esta definido.
es –3. Esto es, cuando
x
= –3, el valor de
y
no esta definido.
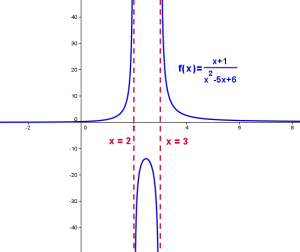
 tiene una asíntota vertical en el valor excluído, o
x
=
b
, y una asíntota horizontal en
y
=
c
.
tiene una asíntota vertical en el valor excluído, o
x
=
b
, y una asíntota horizontal en
y
=
c
. 
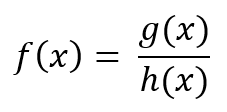




 es la asíntota horizontal.
es la asíntota horizontal.


 es la asíntota oblicua.
es la asíntota oblicua.