Una función racional está definida como el cociente de polinomios en los cuales el denominador tiene un grado de por lo menos 1. En otras palabras, debe haber una variable en el denominador.
La forma general de una función racional es
 , donde
p
(
x
) y
q
(
x
) son polinomios y
q
(
x
) ≠ 0.
, donde
p
(
x
) y
q
(
x
) son polinomios y
q
(
x
) ≠ 0.
Ejemplos:


 y la gráfica es una
hipérbola
.
y la gráfica es una
hipérbola
. 
El dominio y rango es el conjunto de todos los números reales excepto 0.

Valor excluído
En una función racional, un valor excluído es cualquier valor de x que hace al valor de la función y no definido. Así, estos valores deben ser excluídos del dominio de la función.
Por ejemplo, el valor excluído de la función
 es –3. Esto es, cuando
x
= –3, el valor de
y
no esta definido.
es –3. Esto es, cuando
x
= –3, el valor de
y
no esta definido.
Así, el dominio de esta función es el conjunto de todos los números reales excepto –3.
Asíntotas
Una asíntota es una recta que se acerca a la gráfica de la función, pero nunca la toca. En la función padre
 , tanto los ejes
x
y
y
son asíntotas. La gráfica de la función padre se acercará más y más pero nunca tocará las asíntotas.
, tanto los ejes
x
y
y
son asíntotas. La gráfica de la función padre se acercará más y más pero nunca tocará las asíntotas.
Una función racional de la forma
 tiene una asíntota vertical en el valor excluído, o
x
=
b
, y una asíntota horizontal en
y
=
c
.
tiene una asíntota vertical en el valor excluído, o
x
=
b
, y una asíntota horizontal en
y
=
c
. En este artículo te voy a explicar brevemente lo que son las funciones racionales y te mostraré unas funciones racionales ejemplos para que las entiendas mejor.
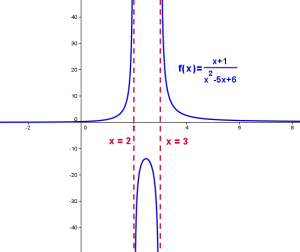
Una función es racional si: en donde g(x) y h(x) son polinomios. El dominio de la función serán todos los números reales con excepción los números en los cuales se hace cero el denominador.
Por ejemplo en una función f (x ) = 1 / x – 2, el dominio es toda x excepto x =2.
Cuando se hace la gráfica de una función racional es importante saber:
- Qué se puede decir de los valores de la función cuando x se acerca a un cero del denominador?
- Qué se puede decir de los valores de la función cuando x es grande y positiva o negativa?
La recta x = a es una asíntota vertical de la gráfica de una función si f (x) –> ∞ o f (x) –> -∞ cuando x tiende a a.
Asíntota horizontal
La recta y = c es una asíntota horizontal de la gráfica de una función si f (x) –> c cuando x –> ∞ o cuando x –> -∞
Video:
https://www.youtube.com/watch?v=1OOrMK1w2Dk
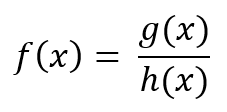
No hay comentarios:
Publicar un comentario