Funciones de grado Superior
Modelo Gráfico
El modelo gráfico es un procedimiento de solución de problemas de programación lineal, muy limitado en cuanto al número de variables, pero muy rico en materia de interpretación de resultados e incluso análisis de sensibilidad. Este consiste en representar cada una de las restricciones y encontrar en la medida de lo posible el polígono (poliedro) factible, comúnmente llamado el conjunto solución o región factible, en el cual por razones trigonométricas en uno de sus vértices se encuentra la mejor respuesta (solución óptima).
1.-Se despeja la incógnita y en ambas ecuaciones
2.- Se construye para cada una de las dos funciones de primer grado obtenidas la tabla de valores correspondientes
3.- Se representan gráficamente ambas rectas en los ejes coordenados
Ejemplo
Lo primero que hacemos es despejar la en ambas ecuaciones.
Primera ecuación:
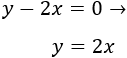
Segunda ecuación:
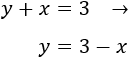
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Utilizaremos y .
Para la primera función tenemos la tabla
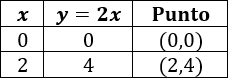
Para la segunda función tenemos la tabla
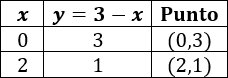
Ahora representamos los puntos de cada tabla uniéndolos:
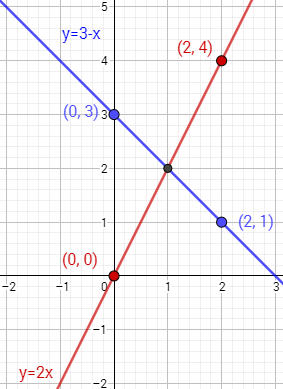
La solución del sistema es el punto donde las gráficas se cortan:
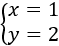
No hay comentarios:
Publicar un comentario